- Introdução
- Rotações e Velocidade
Angular
- Aceleração Radial
- Rotação
com Aceleração Angular Constante
- Relação entre
Velocidade e Aceleração, Lineares e Angulares
- Energia Cinética de
Rotação. Momento de Inércia
- Cálculo de Momento
de Inércia
- Trabalho e Potência
no Movimento Rotacional
- Momento Angular e Impulso
Angular
- Analogia entre Movimento Linear
e Movimento Angular
Aula-7
![]() 1- Introdução
1- Introdução
Neste capítulo iniciaremos o estudo do movimento dos corpos extensos (corpos sólidos), aqueles corpos que não podem ser tratados como tendo toda a massa concentrada em ponto. Um objeto extenso pode mudar tanto a sua posição quanto a sua direção. A Fig.7-1(a) mostra um objeto extenso com apenas o movimento de translação. A Fig.7-1(b) mostra o mesmo corpo em um movimento de translação e rotação. Os objetos estudados, até o momento, não apresentavam movimento de rotação em torno de um eixo próprio. A descrição do movimento de um corpo extenso requer, em geral, três ângulos de orientação assim como as três coordenadas do seu centro de massa. Ao nível introdutório, o qual será considerado aqui, confinaremos nossas atenções ao estudo das rotações de objetos confinados em um plano.

Fig. 7-1 (a) Movimento
translacional puro

Fig. 7-1 (b) Movimento
rotacional puro

Fig. 7-1 (c) Movimento
translacional + rotacional
![]() 2- Rotações e Velocidade Angular
2- Rotações e Velocidade Angular
Quando um corpo sólido gira em torno de um eixo próprio, as coordenadas x, y e z de cada ponto no corpo aumentam e diminuem continuamente a medida que o objeto percorre uma trajetória circular. O use de coordenadas x, y e z, é em geral uma forma complicada de descrever as rotações. Em particular, as rotações confinadas em um plano podem ser facilmente descritas por um ângulo. A maioria de nós é familiar a utilização de medidas envolvendo ângulos (graus e radianos). A escolha de 360 graus para denotar uma revolução completa foi feita pelos babilônios e que provavelmente teve origem nos seus estudos e interesses em astronomia, principalmente na previsão das estações do ano, já que a rotação da Terra em torno do Sol tem aproximadamente 360 dias. Com isto, a rotação de um grau feita pela Terra, em sua órbita, equivaleria a um dia.
Considere o comprimento s do segmento de um círculo contido em ângulo q , como indicado na Fig.7-2(a). Se o círculo tem um raio r, o comprimento de sua circunferência é dado por

Fig. 7-2
A fração de C contida em q é igual a fração de uma de uma revolução completa (360o) contendo em q . Então,
![]()
Dessa forma temos que
Um ângulo em radianos, sendo definido como a razão entre
dois comprimentos é um número puro. Na Fig. 7-2(b), a linha
de referência OP de um corpo em rotação faz um ângulo
q
1 com a linha de referência fixa Ox, em um instante t1.
Num instante posterior t2 o ângulo cresceu para q
2. A velocidade angular média (![]() ) do corpo, no intervalo entre t1 e t2, é
definida como a razão entre o deslocamento angular Dq
= q 2-
q 1 , e o intervalo de tempo D
t = t2- t1 :
) do corpo, no intervalo entre t1 e t2, é
definida como a razão entre o deslocamento angular Dq
= q 2-
q 1 , e o intervalo de tempo D
t = t2- t1 :
![]() 3- Aceleração Angular
3- Aceleração Angular
Se a velocidade angular de um corpo variar, diz-se que ele tem uma aceleração.
Se w 1 e w2
forem as velocidades angulares instantâneas, no tempo t1
e t2 a aceleração angular média ![]() é definida como
é definida como
 ,
(5)
,
(5) ,
(7)
,
(7)![]() 4 - Rotação com Aceleração Angular Constante
4 - Rotação com Aceleração Angular Constante
O caso mais simples de movimento de rotação acelerado é aquele no qual a aceleração é constante. Neste caso, as expressões da velocidade e do deslocamento angulares são facilmente encontradas por integração. Tem-se
![]() ,
,
![]()
![]() .
.
Se w o é a velocidade angular quando t = 0, segue-se que C1 = wo e
cuja solução é
Se o ângulo q tem o valor qo quando t = 0 e se a velocidade angular inicial é wo, então, C3 = aq o- ½wo2 e
|
linear constante |
angular constante |
|
|
|
|
|
|
|
|
|
|
|
|
Tab. 7-1
![]() 5- Relação entre Velocidade e Aceleração, Lineares
e Angulares
5- Relação entre Velocidade e Aceleração, Lineares
e Angulares
Em
seções anteriores estudamos a velocidade e a aceleração
lineares de uma partícula em movimento circular. Quando um corpo
rígido está animado de rotação em torno de
um eixo fixo, cada ponto do corpo descreve um círculo cujo centro
está sobre o eixo de rotação e cujo plano é
perpendicular ao eixo. Existem algumas relações simples e
úteis entre a velocidade e a aceleração angulares
do corpo em rotação e a velocidade e aceleração
lineares dos seus pontos.

Fig.7-3
Seja r a distância do eixo ao um ponto P do corpo que se move sobre uma circunferência de raio r, Fig.7-3. Quando o raio faz um ângulo q com o eixo de referência, a distância s percorrida pelo ponto P é
se q for medido em radiamos. Derivando ambos os membros desta equação em relação a t e tendo em vista que r é constante, vem
 (15)
(15)
Fig.7-4
![]() 6- Energia Cinética de Rotação. Momento de Inércia
6- Energia Cinética de Rotação. Momento de Inércia
Mostrou-se que o módulo de velocidade de uma partícula em um corpo rígido rodando em torno de um eixo fixo é
onde r é a distância da partícula ao eixo e w é a velocidade angular do objeto. A energia cinética de uma partícula de massa m é então,
 (17)
(17)
 (19)
(19)Observando a equação (18) notamos que ela é análoga à expressão da energia cinética translacional:
onde o momento de inércia I é análogo à
massa m (ou inércia), e a velocidade angular (w
) é análoga à velocidade linear (v). Entretanto, o
momento de inércia de um corpo depende da localização
do eixo de rotação, e isto deve ser sempre especificado quando
se descreve um momento de inércia.
Para um corpo que não é composto de massas puntiformes discretas,
mas sim de uma distribuição contínua de matéria,
o somatório usado na definição de momento de inércia
I deve ser calculado pelos métodos do cálculo integral.
A
seguir daremos exemplos de momentos de inércia para algumas distribuições
de massa mais comuns, veja Fig.7-5.





Fig.7-5
Deve-se observar que não é correto, em geral, calcular o momento de inércia de um corpo supondo-se que toda a massa esteja concentrado no centro de massa (centro de gravidade). Por exemplo, quando uma barra fixa e uniforme de comprimento L e massa M gira em torno de um eixo perpendicular a ela, e sua extremidade, o momento de inércia, e I= ML2/3, enquanto se, se supusesse a massa toda concentrada no centro, a uma distância L/2 do eixo, obter-se-ia o resultado incorreto I = M(L/2)2 = ML2/4.
O
conceito de momento de inércia, juntamente com o princípio
geral de trabalho-energia, é muito útil em problemas que
envolvem rotação de corpos rígidos.
![]() 7- Cálculo de Momento de Inércia
7- Cálculo de Momento de Inércia
O momento de inércia pode ser calculado usando-se sua definição dada na equação (19), para qualquer sistema constituído por partículas discretas.
Para um corpo que não é composto de massas puntiformes discretas, mas sim contínua temos que substituir o somatório por uma integral. Imagine o corpo subdivido em elementos de volume, cada qual de massa D m e a uma certa distância r do eixo de rotação. Se cada massa D m é multiplicada pelo quadrado da sua distância ao eixo e todos os produtos r2D m somados sobre todo o corpo, o momento de inércia será dado por
 .
(20)
.
(20)![]() (a) - Momento de Inércia de um Barra Delgada
(a) - Momento de Inércia de um Barra Delgada
A
Fig.7-6 mostra uma barra delgada, uniforme, de massa m e comprimento L.
Deseja-se calcular seu momento de inércia em relação
a um eixo que passa pelo ponto A, a uma distância h de uma das extremidades.
Toma-se para elemento de volume uma pequena seção de comprimento
dx e a seção transversal S, a uma dist6ancia x do ponto.
Então,
 (24)
(24)
Fig.7-6
A partir desta expressão geral, pode-se achar o momento de inércia em relação a um eixo através de qualquer ponto da barra. Por exemplo, se o eixo passa através da extremidade esquerda, h = 0 e
Se o eixo passa através da extremidade direita, h = l e
como era de se esperar. Se o eixo passa no ponto médio (h = l/2), então
![]() (b) Cilindro Oco ou Sólido, Eixo de Simetria
(b) Cilindro Oco ou Sólido, Eixo de Simetria
A Fig.7-7 mostra um cilindro oco de comprimento l, raio interno R1 e externo R2. Escolhe-se como elemento de volume mais conveniente uma fina camada ciíndrica de raio r, espessura dr e de comprimento l. Sendo r a massa específica do material, então,
O momento de inércia é dado por


Fig.7-7
Se a massa específica r do corpo não for constante, precisa-se conhecê-la como função de r, antes de realizar a integração. Para um sólido homogêneo, porém, r é constante e

A massa m do cilindro inteiro é igual ao produto de sua massa específica pelo seu volume. O volume é dado por
![]()
então a massa será
e o momento de inércia (I) é, portanto,
Note
que o momento de inércia de um cilindro em relação
ao um eixo que coincide com o seu eixo de simetria não depende do
comprimento l. Dois cilindros ocos com mesmos raios internos e externos,
um de madeira e o outro de fero, mas tendo a mesma massa, têm momentos
de inércia iguais, embora o comprimento do primeiro seja muito maior.
O momento de inércia só depende da distribuição
radial de massa, não da sua distribuição ao longo
do eixo. Assim, a equação (25) vale também para um
cilindro muito pequeno, como uma arruela.
![]() 8- Trabalho e Potência no Movimento Rotacional
8- Trabalho e Potência no Movimento Rotacional
Uma força aplicada a um corpo em rotação realiza trabalho sobre o corpo. Este trabalho pode ser expresso em termos do torque da força e do deslocamento angular.
Suponha que uma força F atue na periferia de uma roda de raio R, conforme mostra a Fig.7-8, enquanto a roda gira em pequeno ângulo dq . Se este ângulo for suficientemente pequeno, a força poderá se encarada como constante durante o intervalo de tempo correspondentemente pequeno. Por definição, o trabalho da força F é
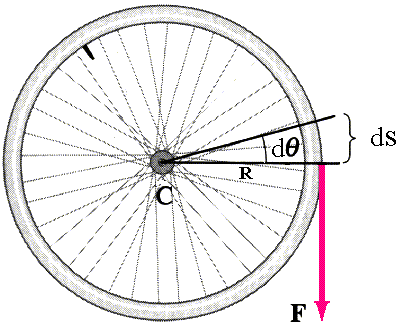
A potência relacionado como movimento rotacional pode ser determinada derivando ambos lados da equação (26) em função do tempo, isto é
ou
Havendo vários torques atuando no corpo, cada um realiza
trabalho e a taxa de variação da energia cinética
total é a soma das potências dos torques individuais, que
é w multiplicada pela soma dos torques.
Assim, no caso geral,
 (30)
(30)
A equação (30) pode ser, também, derivada da segunda
lei de Newton, sem o uso direto da consideração energia.
![]() 9- Momento Angular e Impulso Angular
9- Momento Angular e Impulso Angular
Nas seções anteriores deste capítulo, vimos que se usamos as variáveis angulares apropriadas, a cinemática e dinâmica dos corpos em rotação têm equações equivalentes ao caso dos movimentos lineares ordinários. Anteriormente vimos que a energia cinética rotacional Ec = ½ Iw2 é análoga à energia cinética dos movimentos lineares Ec = ½mv2. De um modo similar o momento linear (momentum) tem também o análogo no caso dos movimentos rotacionais, o qual é chamado momento angular (L), que para um corpo em rotação em torno de um eixo fixo é definido por
A equação para a segunda lei de Newton, no caso de movimentos rotacionais, também é análoga ao caso linear (F = ma), como mostramos a seguir,

ou
 (32)
(32)![]() O momento angular total de um corpo em rotação permanece
constante se o torque resultante agindo sobre o corpo é igual a
zero.
O momento angular total de um corpo em rotação permanece
constante se o torque resultante agindo sobre o corpo é igual a
zero.
A lei de conservação do momento angular é umas das mais importantes leis de conservação da Física. Quando o torque resultante sobre um corpo é igual a zero e o está em rotação em torno de um eixo fixo ou em torno do centro de massa, tal que a sua direção não muda, podemos dizer que
Muitos fenômenos interessantes podem entendidos usando a lei de conservação do momentum angular. Considere, por exemplo, o caso de uma bailarina fazendo um movimento de rotação em torno do seu corpo, Fig.7-9. Se durante o movimento de rotação os seus braços estão abertos a velocidade será menor do que quando os seus braços estiverem juntos ao corpo. Isto pode ser explicado se usamos a definição de momento de inércia I = mr2. É claro que quando os braços são puxados para próximo do corpo da bailarina, o eixo de rotação r é reduzido, consequentemente o momento de inércia diminuirá. Desde que o momento angular permanece constante, se I decresce, então a velocidade angular tem que crescer para manter o momento angular constante (L = Iw = const. ). Se a bailarina reduz o seu momento de inércia por fator 2, então ela rodará com uma velocidade angular duas vezes maior.

Um exemplo similar ocorre com as atletas de saltos ornamentais. Elas usam deste mesmo princípio para girar mais ou menos rápido em torno do seu centro de massa.
Note
que para o momento angular ser conservado é necessário que
o torque resultante seja zero, mas a força resultante não
necessariamente tem quer ser nula. Por exemplo, no caso da atletas de saltos
ornamentais o torque é igual a zero, mesmo tendo uma força
gravitacional atuando sobre ela.
![]() 10- Analogia entre Movimento Linear e Movimento Angular
10- Analogia entre Movimento Linear e Movimento Angular
A
seguir apresentamos uma tabela que resumo e correlaciona o movimento angular
como o translacional.
|
(direção fixa) |
(eixo fixo) |
| Posição x | Posição angular q |
| Velocidade v | Velocidade angular w |
| Aceleração a | Aceleração angular a |
| Massa m | Inércia rotacional I |
| Segunda Lei de Newton F = ma | Segunda lei de Newton t = Ia |
| Trabalho W = Ç Fdx | Trabalho W = Çt dq |
| Energia cinética Ec = ½ mv2 | Energia cinética Ec = ½ Iw 2 |
| Potência P = Fv | Potência P = tw |
| Trabalho-energia cinética W=D Ec | Trabalho-energia cinética W = D Ec |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tab.7-2
|
|
![]() Electronic
Address : kcmundim@unb.br
or spedrosa@fis.ufba.br
Electronic
Address : kcmundim@unb.br
or spedrosa@fis.ufba.br
Last Updated: Jan/24/2000
Copyright 1997: Kleber C. Mundim.
All rights reserved.
Register No 169.766 - Biblioteca Nacional - Ministério
da Cultura