1.  A Mecânica Quântica e o Significado de Y

        Vimos que através das observações experimentais sobre o efeito de interferência no caso da matéria, assim como da luz, tornou-se claro que ambas, matéria e radiação, têm comportamento ondulatório. Por outro lado, o efeito fotoelétrico indica que a luz se comporta como uma coleção de partículas viajando como velocidade c = 300.000 km/s. Estas partículas foram chamadas de fótons. Sabemos também, que os elétrons comportam-se como se fossem partículas, mesmo que eles possam produzir, também, efeitos de interferência. Como podemos reconciliar este aparente conflito? Isto é, tanto a matéria quanto a luz têm comportamentos duais onda-corpúsculo?
        Em 1926, Max Born sugeriu uma unificação pictórica para estes conceitos introduzindo o significado de amplitude de onda de matéria.

    Primeiro, vamos lembrar que a densidade de energia de uma onda eletromagnética, ou energia por unidade de volume, é proporcional ao quadrado de sua amplitude (A² ). Isto pode ser demonstrado usando as equações de Maxwell para o eletromagnetismo. Isto significa que:

 Levando em conta o comportamento corpuscular da luz (fóton), sua energia E = n(hn), onde n é a freqüência da luz e n é o número de fótons. De onde tiramos que:

    Das duas últimas equações vemos que o número de fótons por unidade de volume é proporcional ao quadrado da amplitude da radiação eletromagnética. Isto é,

Esta relação levou Born a assumir que a onda de matéria, representada pela função Y(x,t),  tem uma amplitude tal que o seu quadrado é igual ao número de partículas por unidade de volume,

        De acordo com Schrödinger as propriedades eletrônicas em átomos e moléculas podem ser obtidas resolvendo uma equação, que ficou conhecida como equação de onda de Schrödinger porque ele se baseou na descrição do movimento eletrônico como uma onda. Esta onda não é uma onda que viaja através do espaço como uma onda eletromagnética ou luz, mas é uma onda estacionária que está confinada no átomo ou molécula de forma semelhante às ondas produzidas pelas cordas de um violino.

Leia aqui o artigo original de Schrödinger.

            Estes movimentos possíveis são sempre em múltiplos inteiros de l /2 ou meio comprimento de onda. Assim, podemos dizer que as vibrações de uma corda de violino são quantizadas no sentido de que somente certas vibrações são permitidas. Os pontos nos quais a amplitude da onda é zero são denominados de nodos. Excluindo os pontos nos extremos fixos da corda, a vibração de mais baixa energia tem zero nodo. O segundo estado vibracional de mais baixa energia tem um nodo, o segundo dois nodos e assim sucessivamente. Dessa forma podemos representar os estados vibracionais por um número inteiro n. Para o caso de mais baixa energia n = 1, o próximo, n = 2, e assim sucessivamente. Em geral, as vibrações têm n - 1 nodos.

        Por outro lado, de acordo com os postulados da teoria quântica o movimento eletrônico no átomo é ondulatório, sendo as ondas estacionárias, e podem ser descritos de forma equivalente ao movimento das cordas do violino. Isto é, as ondas eletrônicas são do tipo estacionárias. Neste sentido a solução da equação de Schrödinger deve contemplar os postulado da mecânica quântica, discutidos anteriormente, e estabelecer a quantização das energias e, conseqüentemente, das órbitas eletrônicas. No caso de átomos, estas ondas estacionárias são denominadas de orbitais. Como o movimento eletrônico é descrito em um espaço tri-dimensional são necessários três números quânticos (n, l e m) para descrever os orbitais atômicos. Os nodos circulares e lineares no movimento bidimensional são agora substituídos por uma superfície nodal a qual pode ser planar ou esférica (veja Fig.2). O número total de nodos continua sendo n-1. O número de nodos planares é dado pelo número quântico l, o qual como antes, podem assumir qualquer número inteiro entre 0 e n-1. O número de nodos esféricos ou circulares é, portanto, igual a n-1-l.

     A função de onda pode ser obtida por analogia com um problema conhecido de Mecânica, aquele dos modos naturais de vibração de uma corda de comprimento d, fixa em uma de suas extremidades, como mostra a Fig.1. As condições de contorno de uma corda vibrante impõem que em cada extremidade haja um nó. Isso significa que o comprimento de onda l deve ser escolhido de tal forma que

o que implica na quantização do comprimento de onda l.

    A perturbação ondulatória de uma corda é representada por uma onda estacionária, cuja dependência espacial e temporal é Asen(kx-wt), onde A é uma constante e k = 2p /l é o número de onda. Visto que l é quantizado, k também deverá ser, isto é,

o que nos leva a

                                                                               (1)

A partícula não pode ter uma energia qualquer, como seria de se esperar classicamente, mas apenas os valores dados por E. Dessa forma a onda de matéria pode ser descrita, em estrita analogia com a equação (1) por

    Max Born foi o primeiro a sugerir que o valor da grandeza Y² em um ponto qualquer exprimia a probabilidade da partícula estar próxima desse ponto. Mais exatamente, considerando-se um elemento de volume V que contenha esse ponto, a probabilidade da partícula ser aí encontrada, num dado instante, é dada por Y²V. Esta interpretação de Y fornece uma conexão estatística entre a partícula e onda a ela associada; diz-nos onde a partícula provavelmente estará e não onde, de fato, está.

Fig.2   - Representação da função de probabilidade Y²

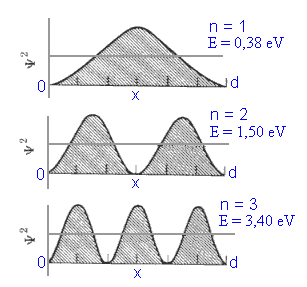
No caso de uma partícula confinada entre paredes rígidas, a probabilidade de se achar a mesma entre dois planos situados a uma distância x e x+ de uma das paredes, num instante t =0,  (ver Fig.2) é dada por

Logo, a densidade de probabilidade é dada por

        A idéia de estados estacionários dos átomos corresponderem a ondas estacionárias de matéria foi usada por Erwin Schrödinger, em 1926, como base da Mecânica Quântica Ondulatória, que é uma das várias formulações equivalentes da Física Quântica. Uma importante grandeza na Mecânica Ondulatória é a função de onda Y , que mede a perturbação ondulatória das ondas de matéria. No caso das ondas produzidas em cordas, a perturbação ondulatória pode ser avaliada pela elongação y; no das ondas sonoras pela variação da pressão e no das ondas eletromagnéticas, pelo vetor campo elétrico E.

        Com a equação de onda tridimensional proposta por Schrödinger, o problema do átomo de hidrogênio, assim como as questões relacionadas com a velha teoria atômica de Bohr, foram corretamente resolvidas. A equação de onda de Schrödinger é uma equação com derivadas nas variáveis espaciais e temporal, a qual, para o caso de independência com o tempo, é expressa pela relação;

Veja no Apêndice mais detalhes sobre esta equação :  Apêndice (não será usado na avaliação)
 

2.  Densidade Eletrônica e o Módulo de y

        Vimos anteriormente que, de acordo com os postulados de Born, a função de onda Y não tem significado físico, mas o seu quadrado representa a densidade de probabilidades de se encontrar o elétron (partícula) em uma dada região do espaço delimitada pelo elemento de volume dV. O módulo ao quadrado de Y, no caso atômico, representa também a densidade eletrônica que descreve as regiões, em torno do núcleo, mais prováveis de se encontrar os elétrons.
        No caso do átomo de hidrogênio, átomo mono-eletrônico,  Y² representa a densidade de probabilidade de se encontrar o elétron em uma dada região em torno do núcleo. O diagrama superior da Fig.3 mostra onde a amplitude da onda tem valores positivos e onde tem valores negativos. Na equação de Schrödinger a amplitude da onda é dada pela função de onda y . Assim, como os orbitais s têm simetria esférica, a variação de y é a mesma em todas a direções, tendo o núcleo na origem da esfera. A forma do orbital 2p pode ser representada, aproximadamente, por uma esfera dividida em duas partes, uma negativa e outra positiva, com o nodo planar sobre o núcleo.

       Em discussões anteriores vimos que a nova teoria quântica foi derivada com base na teoria ondulatória. No sentido de mostrar a analogia entre as duas teorias apresentamos abaixo uma figura que descreve as ondas estacionárias bidimensionais produzidas por um tambor ao ser tocado. Em seguida apresentamos o seu análogo para o caso atômico. No caso de ondas mecânicas a amplitude da onda é uma medida do deslocamento da superfície do tambor.
        A todo instante vimos fazendo uma analogia entre o movimento das ondas estacionárias clássicas com as ondas estacionárias para o elétron no átomo, descrita pela função de onda y . Então podemos perguntar: Qual é o significado da amplitude da onda eletrônica y ? Surpreendentemente y não tem significado físico, mas o valor de y² dá a probabilidade de se encontrar o elétron em um dado ponto do espaço. A variação de y² é bem similar a variação de y , exceto que y² é positiva ou zero para todos os pontos. Podemos fazer um diagrama similar ao da Fig.2 para representar a variação de y², veja Fig.4.

        Estes resultados leva-nos a pensar sobre a carga eletrônica como se ela estivesse espalhada em torno do núcleo. Neste caso a densidade de carga não é uniforme e ela é representada pelo quadrado da função de onda y , isto é y². Esta representação é freqüentemente denominada por nuvem eletrônica. As figuras abaixo mostram um representação esquemática desta nuvem eletrônica.

Fig. 4  Representação gráfica do módulo de y²

 Fig 5 -Diagrama de pontos para a densidade eletrônica
dos orbitais s e p.

        No orbital 1s a densidade de carga (nuvem eletrônica) decresce à medida que se afasta do núcleo. Isto significa que a probabilidade de encontrar o elétron em um dado ponto do espaço diminui a medida que se afasta do núcleo. No caso do orbital 2s a densidade diminui à medida que se afasta do núcleo e fica igual a zero no ponto nodal. Em seguida, aumenta até atingir um ponto de máximo e decresce novamente.
        A densidade de carga para o orbital 2p_z consiste de duas nuvens que têm a forma de uma esfera achatada, sendo um posicionado acima do plano nodal e o outro, abaixo, veja Fig. 6.

3.  Tipos de Orbitais Atômicos para o Átomo de Hidrogênio
 

        Os orbitais atômicos são caracterizados pelos números quânticos discutidos acima, de onde tiramos que;

Orbitais para o qual l = 0 têm somente nodos esféricos e são chamados de orbitais s. Então para n =1 existe um orbital 1s com zero nodos, para n = 2 existe um orbital 2s, n = 3 um orbital 3s e assim sucessivamente.

Orbitais para o qual l = 1 têm um nodo planar e são chamados de orbitais p. Existem também, orbitais 2p com um nodo planar e zero nodos esféricos e orbitais 3p com um nodo planar e um nodo esférico e, assim, sucessivamente.

Orbitais para o qual l = 2 têm dois nodos planares e são chamados de orbitais d. Os orbitais d têm dois nodos planares e zero nodo esférico.

        De acordo com a solução da equação de Schrödinger para o átomo de hidrogênio, a energia dos orbitais dependem somente dos valores de n, e portanto eles crescem em energia na ordem;

        Os orbitais com nodos planares podem ter diferentes orientações relativas no espaço. Por exemplo, o nodo planar em um orbital p pode ser perpendicular a um dos eixos x, y e z. Então existem três orbitais p independentes, os quais são designados por p_x , p_y e p_z. Para qualquer orbital o número de possíveis orientações independentes é dado pelo número de valores que o terceiro número quântico (m) pode assumir, isto é

        Os valores possíveis dos números quânticos n, l e m estão representados na tabela,
 
 

4- Camadas e subcamadas
 

        Todos orbitais relativos a um valor de n são ditos formar uma única camada no átomo. No átomo de hidrogênio todos orbitais, para um mesmo valor de n, têm o mesmo valor de energia, de acordo com a equação (1).

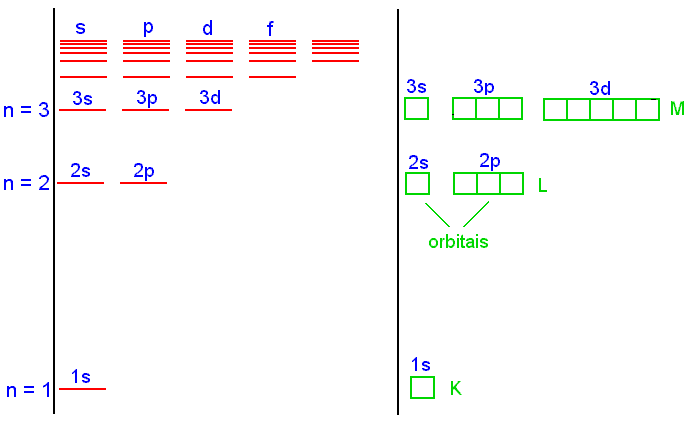
Densidade de probabilidade em função dos números quânticos n, 

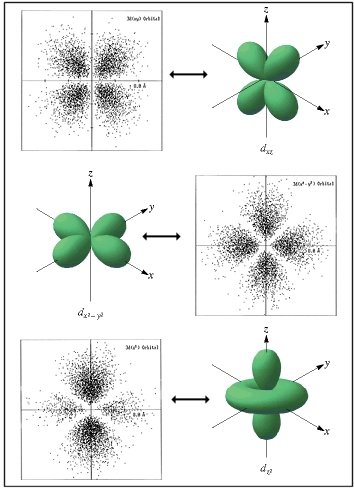
  Densidades de probabilidades relativas aos orbitais tipo d

5- Orbitais do tipo s

        O orbital com  é dito representar o estado fundamental ou de mais baixa energia o qual é descrito pela função de onda;

Como este orbital depende apenas da coordenada r então, ele é um orbital esfericamente simétrico. Já o orbital 2s é descrito pela equação;

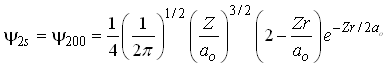
Generalizando, podemos dizer que todos os orbitais do tipo s são dependentes apenas da coordenada r e são portanto esfericamente simétricos.

Em particular o orbital 2s tem um nó, isto é a função de onda tem um ponto em que ela é igual a zero, isto é  Isto implica que,

Assim   é o ponto onde a função de onda se anula, isto é, o ponto onde ela tem um nó.

Orbitais Atômicos

Voltar à página principal

Voltar ao início da página

    O conteúdo desta página está em constante atualização.
Correções no texto e sugestões serão bem vindas.

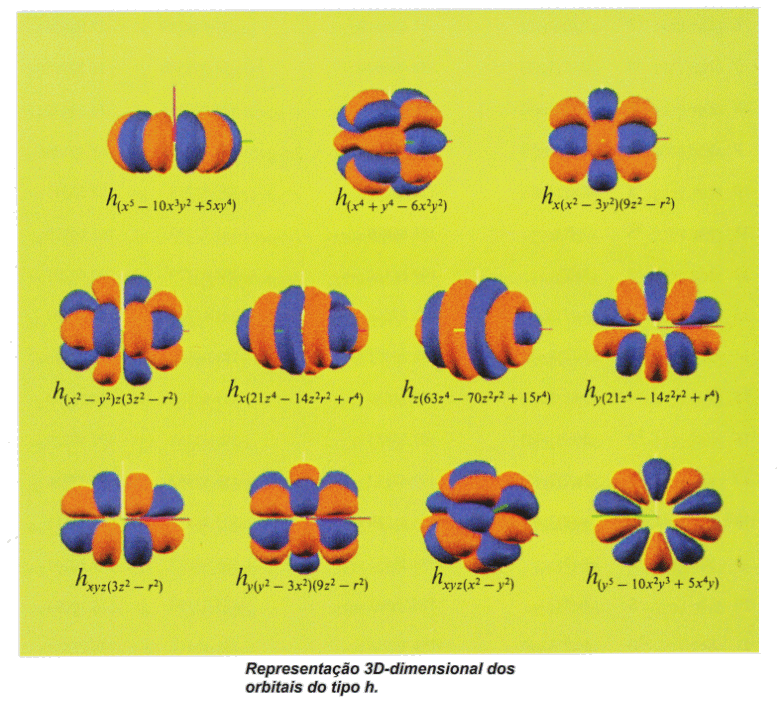
Enviar mensagens para : kcmundim@unb.br
Last Updated: Jan/23/2002
Copyright 1997: Kleber C. Mundim. All rights reserved.
Chemistry Institute-UnB, Brasília  BRAZIL
Register N^o  169.766 - Biblioteca Nacional - Ministério da Cultura